3.2. Drainage models

0D model of drainage

Modelling the drainage of water throughout a catchment area is very complicated. We need to know the capacity of the system to store water and how water flows in and out. On real terrain, the ground may be irregular and so the way in which water flows through it and is stored will be difficult to model.

Given this heterogeneity in the terrain typical in many catchments, it is helpful to first develop an averaged description of the run-off flow from a localised area of the catchment. Eventually, we can add these together as shown in the figure of the multiple drainage zones which flow into the main river.

But first, we therefore work with an integrated picture of the volume of surface water, and relate this to the net run-off flow with a 0D model, with no spatial component. We can consider this a “bucket model” of the drainage basin, as shown in Fig. 3.8.

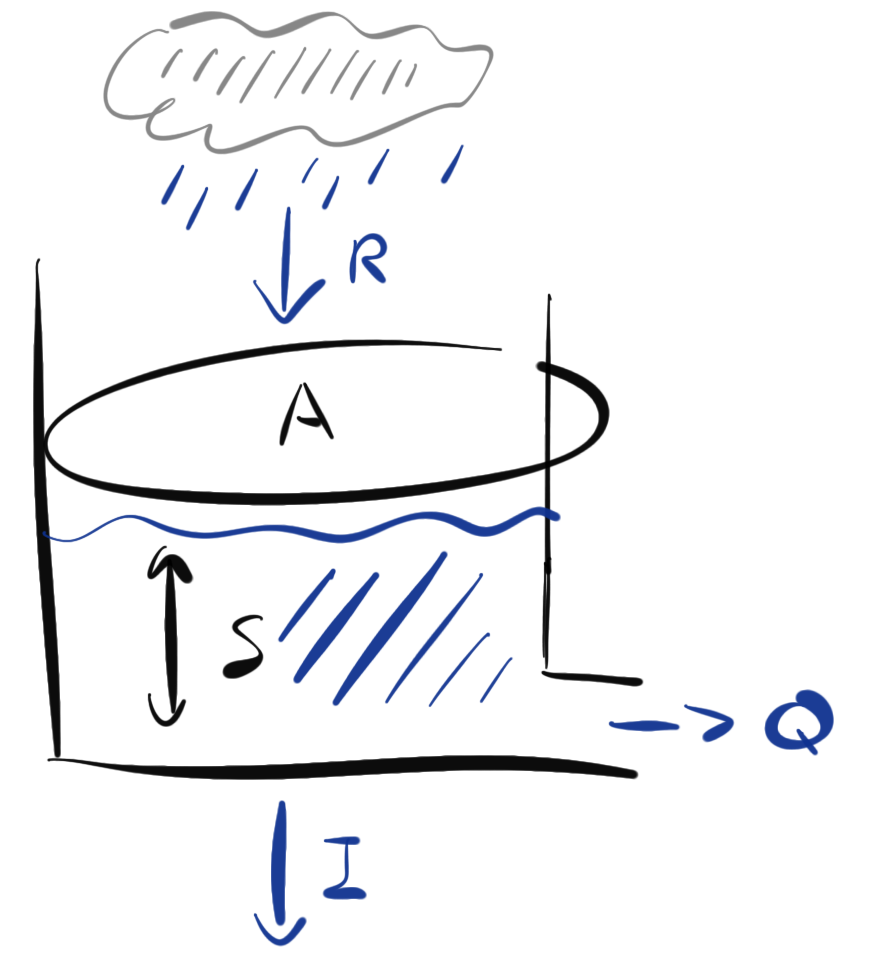
Fig. 3.8 Schematic of the 0D (or “bucket”) model of surface water drainage, over an area \(A\), with an average water depth of \(S\), an input of water due to rainfall at a rate \(R\) per unit area, and fluxes out due to flow into a stream and infiltration (per unit area), \(Q\) and \(I\) respectively.

In this model we will consider the catchment area as a single bucket that accounts for the surface water stored in the area. This bucket has a single input of water due to rainfall, \(F_{in} = RA\), where \(R\) is the (constant) rainfall rate, and \(A\) is the surface area of the watershed. The volume of water stored in the bucket will be \(V = SA\) where \(S\) is the (averaged) depth of water stored in our conceptual bucket.

The fluxes out of the box will be due to infiltration (per unit area) into the soil, a constant \(I\), and a flux out proportional to the amount stored in the bucket \(Q = \lambda V\), where we have not yet identified our constant of proportionality \(\lambda\).

Units!

\[\begin{split} \lambda &= \mathrm{unitless} \\ \end{split}\]

Balancing the fluxes in and out of the system, we can develop an expression for how the volume stored in the system varies with time

(3.1)\[\dv{V}{t} = RA – IA – \lambda V\]

and if we recognise that the surface area of our catchment is constant with time, and dividing through by a factor of that area we get

(3.2)\[\dv{S}{t} = (R – I) – \lambda S\]

We have ignored losses due to evapotranspiration, however we could readily include this in the model, provided we have a relation between evapotranspiration and the rain fall. In heavily vegetated zones this would be a significant process, and the vegetation would also impact the value of \(\lambda S\), the surface run-off rate, since it baffles the surface runoff.

We expect that the water flows from the surface into a network of small drainage channels which then coalesce into larger channels, and eventually flow into a tributary. The simple parameterisation is designed to capture the flow over the surface in a simple fashion including the roughness of the surface, the slope and the vegetation. In the example sheet we explore a nonlinear flux law, but the simple model provides a useful framework for interpreting how a simple drainage system operates.

We now develop our simple, 0D model further to find a solution describing how the water stored \(S\), varies in time. Assuming a constant rainfall and infiltration rate, we can apply an integrating factor \(e^{\lambda t}\) to get the solution

Units!

\[\begin{split} R &= \mathrm{m~s^{-1}} \\ \end{split}\]

(3.3)\[S(t) = S(0) e^{-\lambda t} + \frac{R-I}{\lambda} \left(1 - e^{-\lambda t} \right) dt\]

where the term \(S(0)\) accounts for the initial volume of water stored in the system.

If the rain is finite in duration (a duration \(T\), for example) then the above solution applies for \(0<t<T\). When the rain stops (i.e. for \(t<T\)), we lose the rainfall term, and are just left with the infiltration and flux out, giving us the form

(3.4)\[S(t) = S(T) e^{-\lambda (T-t)} - \frac{I}{\lambda} \left(1 - e^{-\lambda (T-t)} \right)\]

and in this expression \(S(T)\) is evaluated as in (3.3). Since we have prescribed the surface runoff flow from the land to the river to be \(\lambda S\), by assessing the value of \(S\) at any given time we can evaluate the runoff rate.

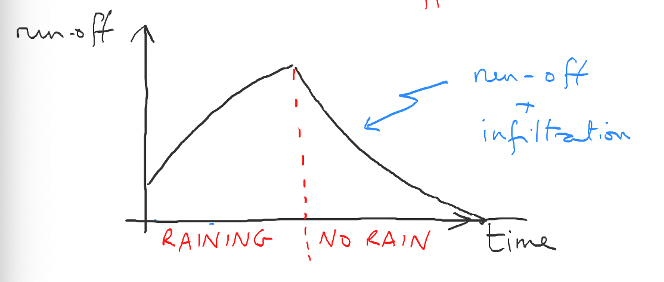
Fig. 3.9 Plot showing the response of the run-off rate to constant rainfall.

1D model of drainage into a river

In a catchment there are a series of drainage zones, each flowing into a stream and then into the river, in a hierarchical way. This leads to the question of how to build a model for the whole drainage basin which is more complex than the idealised bucket model. We also may use such a detailed model to assess the value of \(\lambda\) in the model based on the more detailed physical processes in a more complete model. To this end we consider the next step of development of the model which is to consider the drainage along the land from the watershed to a stream as shown in Fig. 3.10.

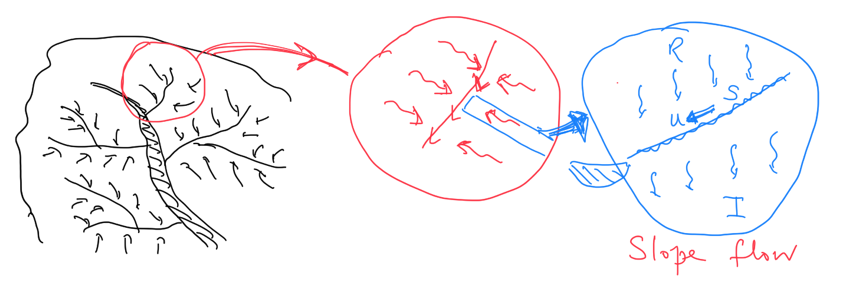
Fig. 3.10 A more detailed surface drainage model showing the fractal nature of drainage networks.

Flow speed

Extending our model from 0D into 1D, adding a spatial dependence, we are going to need to assess the dominant controls on the fluid dynamics. The speed of the flow down the slope may be given in terms of the permeable flow relation; D’Arcy’s law, which we discussed in Section 2.2. Flow through crops, wooded land or other surfaces provide the effective porous media with an effective permeability, \(k\).

In this case, the flow speed will be of the form

Units!

\[\begin{split} u &= \mathrm{m~s^{-1}} \\ \rho &= \mathrm{kg~m^{-3}} \\ g &= \mathrm{m~s^{-2}} \\ \theta &= \mathrm{radians} \\ \mu &= \mathrm{kg~m^{-1}~s^{-1}} \\ k &= \mathrm{m^2} \\ \end{split}\]

(3.5)\[u = \rho g \sin{(\theta)} \frac{k}{\mu}\]

over the surface. The effective permeability may be quite high near the ground.

Deriving the advection equation

We now wish to derive a relation describing how water is stored on and moves down our slope. We will do this by considering the flow of water into and out of a small space element on our slope, \(\delta x\), as shown in Fig. 3.11.

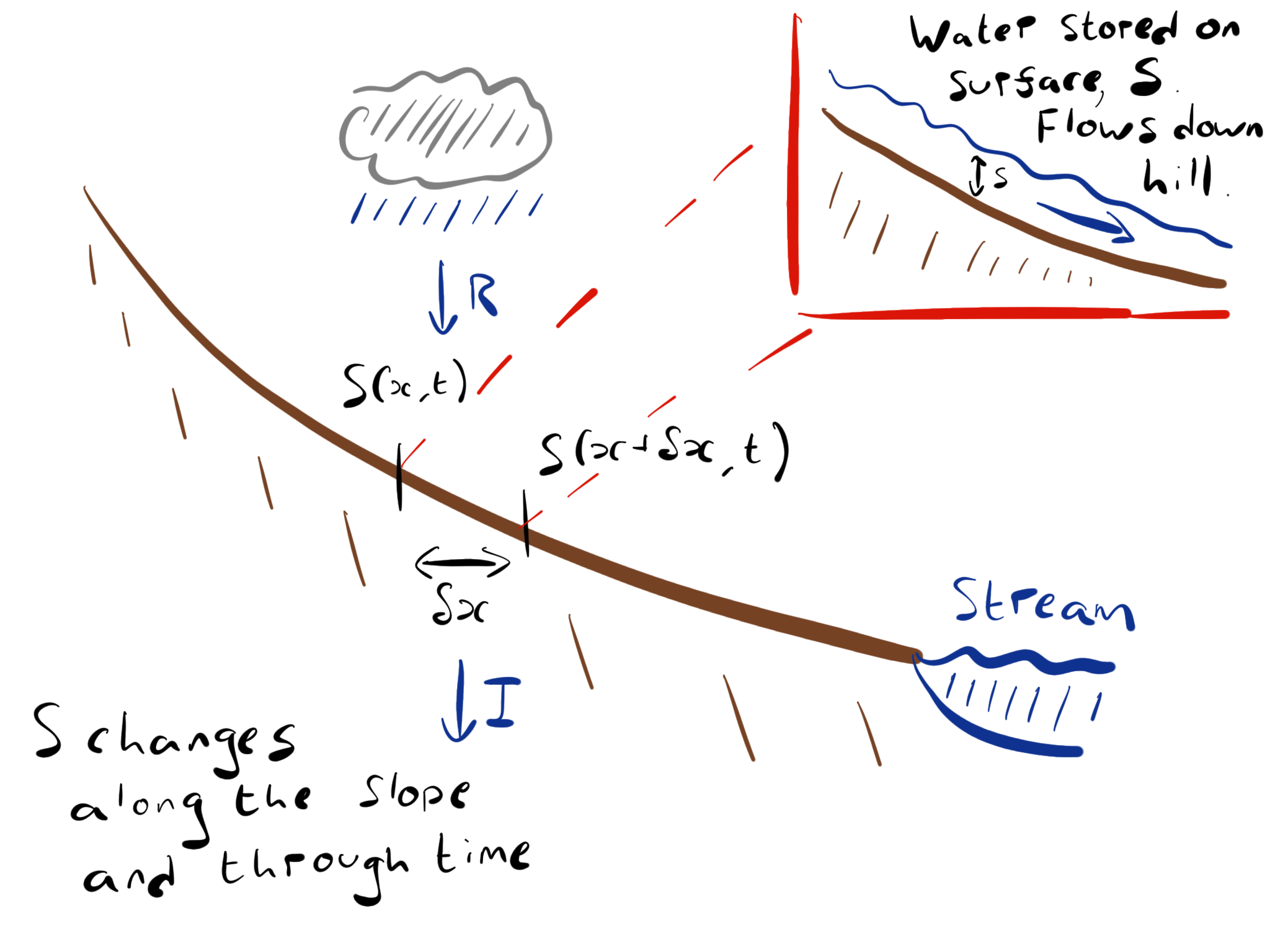
Fig. 3.11 A schematic model showing how surface water, \(S\), flows downhill towards a stream.

The total amount of water stored in our space element is denoted by \(S\). The sources of water to our element will be flow in from up slope, and rain, \(R\). The sinks of water from our element will be flow out of the element down slope, and infiltration into the ground, \(I\).

The flow, \(Q(x,t)\), at a point is calculated as the product of the amount of water \(S\), multiplied by its speed \(u\). Given that our speed down the slope, \(u\), is constant in this formulation, we can use our diagram in Fig. 3.11 to identify the flow in from up-slope as \(u S(x,t)\) and the flow out down-slope as \(-u S(x+\delta x, t)\).

Therefore, balancing all inputs and outputs of water to our space element over a short period of time, \(\delta t\), we get the relation:

Units!

\[\begin{split} Q &= \mathrm{m^3~s^{-1}} \\ R, I &= \mathrm{m~s^{-1}} \\ S &= \mathrm{m^2 \ (m^3 m^{-1})} \\ L &= \mathrm{m} \\ \end{split}\]

\[(S(x, t + \delta t) - S(x, t)) \delta x = R \delta x \delta t - I \delta x \delta t - (u S(x + \delta x, t) - u S(x, t)) \delta t\]

And so dividing through by \(\delta x\) and \(\delta t\), and then taking the limit in which \(\delta x\) and \(\delta t\) go to zero gives us the differential equation

(3.6)\[\frac{\partial S}{\partial t} = R - I - u \frac{\partial S}{\partial x}\]

This is called the advection equation and it governs the change of surface storage along the surface from the watershed to the stream (in the direction of the flow along the surface).

Solving the advection equation

To find the flux of water into the river, we need to evaluate \(S(x,t)\) at the river edge (i.e \(x=L\)). Therefore we need to solve the advection equation. Given that the advection equation has a characteristic speed \(u\), we expect solutions that encode this. In order to use this intuition, we can apply a coordinate transform that moves us into the frame of reference of a parcel of water moving down the slope at a speed \(u\).

Units!

\[\begin{split} W &= \mathrm{m} \\ \eta &= \mathrm{m} \\ \tau &= \mathrm{s} \\ \end{split}\]

\[S(x,t) = W(\eta, \tau)\]

Where \(\eta = x - u t\) and \(\tau = t\).

This leads to the relations:

\[\begin{split}\begin{align} \frac{\partial W}{\partial t} &= - u \frac{\partial W}{\partial \eta} + \frac{\partial W}{\partial \tau} \\ \frac{\partial W}{\partial x} &= \frac{\partial W}{\partial \eta} \end{align}\end{split}\]

Derivation

We want to derive the new derivative relations for our coordinate transformation, Therefore, writing out the total derivative in \(W\):

\[\dd{W} = \pdv{W}{\tau} \dd{\tau} + \pdv{W}{\eta} \dd{\eta}\]

We can then “divide through by \(\dd{t}\)”, which while not rigorous, is fine for a physical system like this one

\[\pdv{W}{t} = \pdv{W}{\tau} \pdv{\tau}{t} + \pdv{W}{\eta} \pdv{\eta}{t}\]

Then evaluating the derivatives of our coordinate transform

\[\pdv{\tau}{t} = 1 \quad \pdv{\eta}{t}=-u\]

and then substituting into our previous equation gives the required result

\[\pdv{W}{t} = \pdv{W}{\tau} - u \pdv{W}{\eta}\]

We could then repeat this analysis to get the equivalent result for \(\pdv{W}{x}\).

Substituting these relations into (3.6) we get

\[\frac{\partial W}{\partial \tau} = R - I\]

We can solve this equation by integrating with respect to \(\tau\) (recalling \(R\) and \(I\) are constant). This gives us a solution for a given (i.e. constant) value of \(\eta\).

\[W(\eta, \tau) = W(\eta, 0) + (R - I) \tau\]

Where \(W(\eta, 0)\) is our constant of integration representing the initial condition. This allows us to construct a characteristic diagram for the system, showing solutions in the \(x\) - \(t\) plane, along lines of constant \(\eta\). This is shown in Fig. 3.12.

We want the solution when \(x = L\) (i.e. the value of \(S\) at the stream), shown as the dashed line intersecting the \(x\) axis in Fig. 3.12.

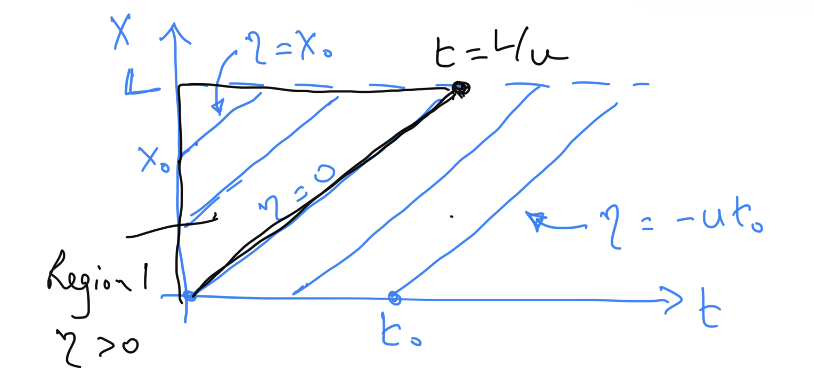
Fig. 3.12 The characteristic diagram for the advection equation, showing lines of \(\eta = \mathrm{constant}\) on the \(x\) - \(t\) plane.

There are two regions for the solution:

• Region 1. The set of points where \(x = L\) and \(t \lt \frac{L}{u}\), for which lines \(\eta = \mathrm{constant}\) start on the x-axis at time = 0 (e.g. the line starting at \(x_0\)). For each of these lines, the time at which they reach the distance \(x = L\) is \(t = \frac{(L-x_0)}{u}\); i.e. the time for the line of constant \(\eta\) starting at \(x=x_0\) at \(t=0\) to reach the line \(x = L\). Therefore the value of \(W\) (and hence \(S\)) at time \(t\) and at \(x = L\) is \(W=(R-I)t\).

• Region 2. The other region corresponds to the points \(x=L\) and \(t \gt \frac{L}{u}\). In this region the lines of constant \(\eta\) which reach \(x = L\) for \(t \gt \frac{L}{u}\) start at \(x = 0\) at a time \(t_0 \gt 0\). Hence, the time to reach the line \(x = L\) is \(\frac{L}{u}\), and so at \(x = L\), \(W = (R-I) \frac{L}{u}\) for \(t \gt \frac{L}{u}\).

As a result, the flux at \(x = L\) is given by

\[\begin{split}\begin{align} u S &= u (R - I) t && \mathrm{for} && t \lt \frac{L}{u}\\ u S &= (R - I) L && \mathrm{for} && t \geq \frac{L}{u} \end{align}\end{split}\]

Matching this latter solution for equilibrium with the equilibrium solution for the bucket model, we can identify the parameter \(\lambda\) in the bucket model as

\[\lambda = \frac{L}{u}\]

This is the time constant for reaching equilibrium between the surface water accumulation and flow into the streams.