3.5. Flood waves

We now turn our attention to the propagation of flood waves down a river. This is important to predict since it is useful to know the time of arrival of a flood many tens of kilometers downstream in order to provide warning to residents and try to mitigate the impacts, but also for planning flood prevention systems for example.

We consider a storm that adds an impulse of water to a river of volume \(V\), moving down a river of area \(A\), at a speed \(u\). This gives a flux of water downstream \(Q=uA\). This situation is shown in Fig. 3.21.

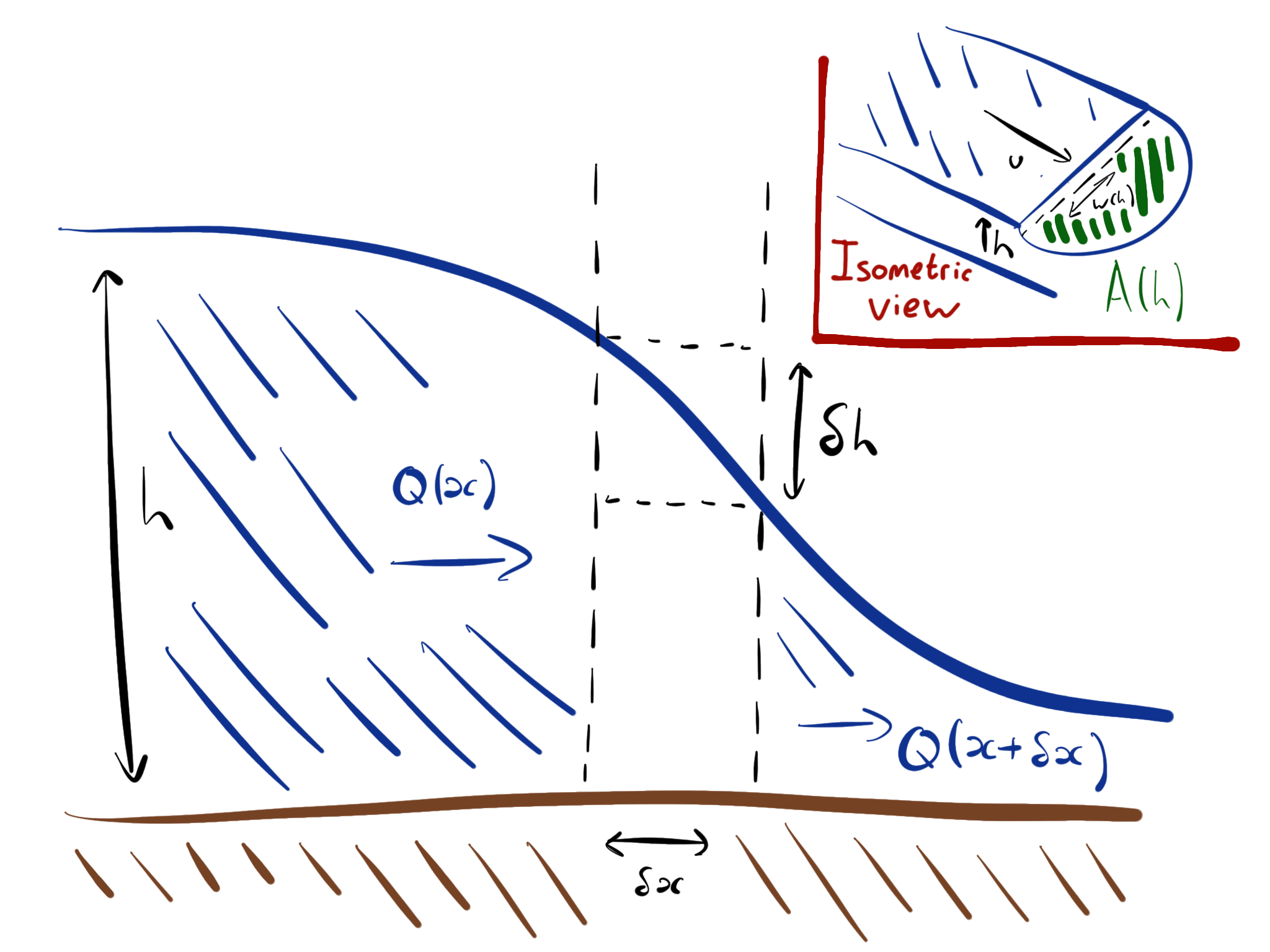
Fig. 3.21 Schematic showing an impulse of water from a storm moving downstream.

If we take the width of the river to be \(W(h)\), then we can relate the change in water volume across a small distance \(\delta x\) to the flux in and out

(3.20)\[\begin{split}\begin{align} W(h) \delta h \delta x = &\ Q(x) - Q(x + \delta x) \delta t \\ W(h) \frac{\delta h}{\delta t} = &\ - \frac{\delta Q}{\delta x} \\ W(h) \pdv{h}{t} = &\ - \pdv{Q}{x} \end{align}\end{split}\]

If we then choose, for the sake of this derivation, a triangular river geometry like that in Section 3.3 where \(A(h) = \alpha h^2\) and \(W(h) = \beta h\). We recall from Section 3.3 that for a triangular river, \(Q = k h^\frac{5}{2}\). we can substitute this into (3.20) by first evaluating \(\pdv{Q}{x}\):

\[\pdv{Q}{x} = \pdv{Q}{h} \pdv{h}{x} = \frac{5}{2} k h^\frac{3}{2} \pdv{h}{x}\]

and with that result now substituting into (3.20)

(3.21)\[\begin{split}\begin{align} \beta h \pdv{h}{t} + \frac{5}{2} k h^\frac{3}{2} \pdv{h}{x} = &\ 0 \\ \pdv{h}{t} + \frac{5k}{2 \beta} h^\frac{1}{2} \pdv{h}{x} = &\ 0 \end{align}\end{split}\]

This is analogous to the advection equation we derived in Section 3.2, except this time the characteristic speed \(u\) has been replaced with an expression for the speed that is dependent on the height; \(\frac{5k}{2 \beta} h^\frac{1}{2}\). Therefore, we expect there is a solution for lines of constant height moving down the channel with speed that depends on their depth. Conceptually, this should look like the diagram shown in Fig. 3.22. We are implicitly ignoring the curving over of wave tops that is a familiar feature of breaking waves. This is a very complicated phenomena to model, and doesn’t serve our purposes here to model. We assume that any over-steepened wave instantly breaks, as shown in the lower panel of Fig. 3.22.

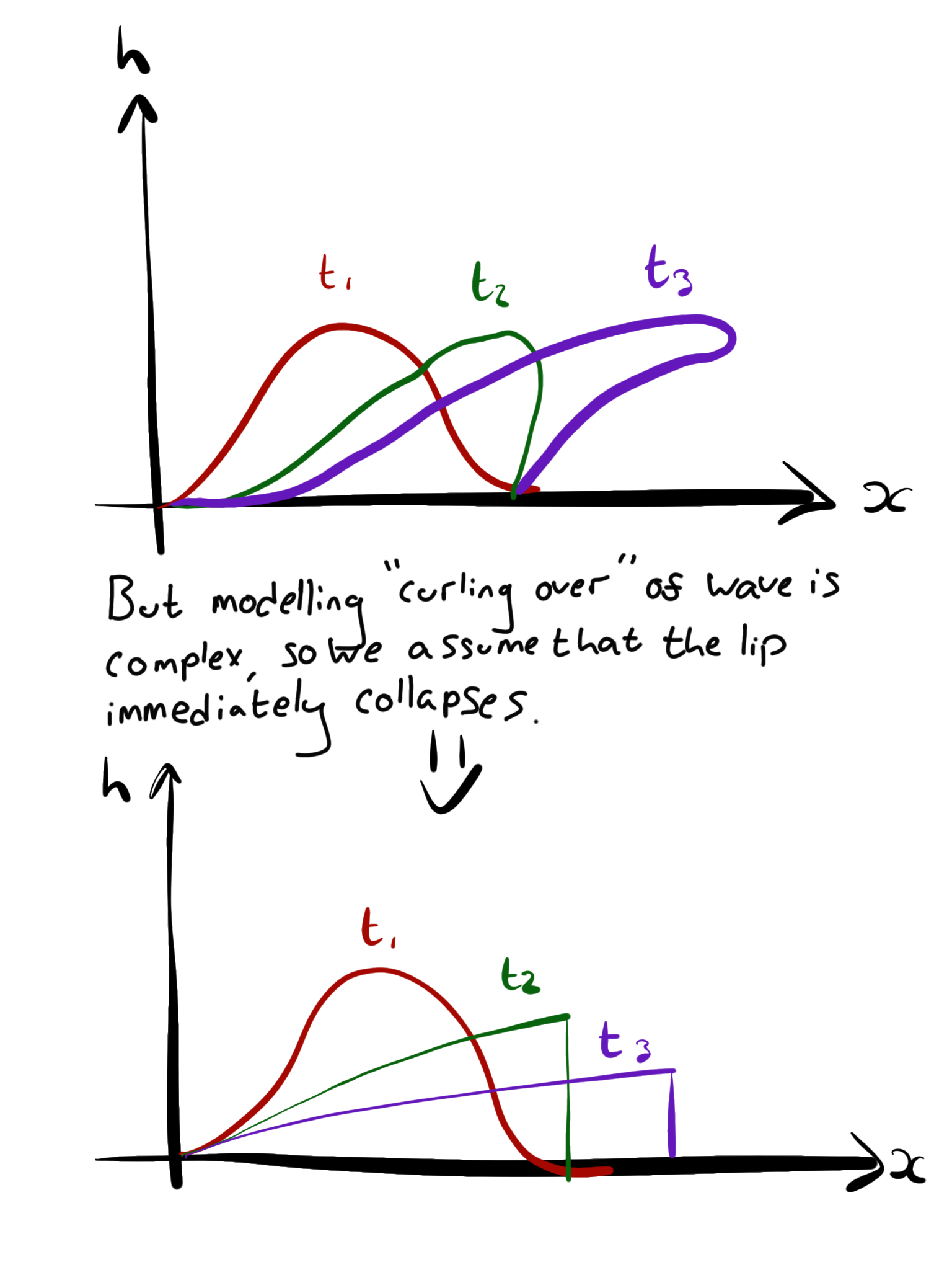
Fig. 3.22 Top: Sketch of the shape of the flood wave nose inferred from the form of the differential equation governing the system. Bottom: Sketch of the shape of the floodwave nose assuming that any over-steepened waves instantly break. The flood wave gets longer and thinner.

We now use the same approach we applied to the advection equation solution in Section 3.2 and try a solution of the form:

\[h(x,t) = Z(x - \frac{5k}{2 \beta} h^\frac{1}{2} t, \tau)\]

i.e. a coordinate change, so that we are now in the frame of reference of the wave (\(\eta\) moves at the speed of a line of constant height \(h\))

\[\eta = x - \frac{5k}{2 \beta} h^\frac{1}{2} t \mathrm{,} \quad \tau=t\]

So then calculating our new derivatives:

\[\begin{split}\begin{align} \pdv{h}{x} = &\ \pdv{Z}{\eta} \pdv{\eta}{x} + \pdv{Z}{\tau} \pdv{\tau}{x} \\ = &\ \pdv{Z}{\eta} \end{align}\end{split}\]

\[\begin{split}\begin{align} \pdv{h}{t} = &\ \pdv{Z}{\eta} \pdv{\eta}{t} + \pdv{Z}{\tau} \pdv{\tau}{t} \\ = &\ \pdv{Z}{\eta} \left(- \frac{5k}{2 \beta} h^\frac{1}{2} \right) + \pdv{Z}{\tau} \end{align}\end{split}\]

Substituting all of this into (3.21) gives us

\[\begin{split}\pdv{Z}{\eta} \left(- \frac{5k}{2 \beta} h^\frac{1}{2} \right) + \pdv{Z}{\tau} + \frac{5k}{2 \beta} h^\frac{1}{2} \pdv{Z}{\eta} = 0 \\ \implies \pdv{Z}{\tau} = 0\end{split}\]

Which means that \(Z\) is constant (i.e. depth is constant) provided we move along a line on which \(\eta\) is constant. So examining one possible solution, for which \(\eta = 0\), we get

\[x = \frac{5k}{2 \beta} h^\frac{1}{2} t \quad \quad h = \mathrm{const.}\]

Rearranging this then gets us to

(3.22)\[h = \left( \frac{2 \beta}{5k} \right)^2 \frac{x^2}{t^2}\]

Using this solution for the long time depth of the current, we can estimate the nose location and depth (see Fig. 3.22 for a reminder of what this looks like).

Applying the conservation of fluid, we first work out the volume in the flow and this leads to an expression for the position of the nose:

(3.23)\[V = \int_0^{x_N} A(h(x,t)) \dd{x}\]

where \(x_N\) is the position of the flood wave nose. We note that

(3.24)\[A = \int_0^{h} W(h') \dd{h'} = \frac{1}{2} \beta h^2\]

and substituting (3.22) and (3.24) into (3.23) we get

\[\begin{split}\begin{align} V = &\ \int_0^{x_N} \frac{1}{2} \beta \left(\frac{2 \beta}{5k} \right)^4 \frac{x^4}{t^4} \dd{x} \\ = &\ \frac{1}{2} \beta \left(\frac{2 \beta}{5k} \right)^4 \frac{x_N^5}{5 t^4} \end{align}\end{split}\]

We can then rearrange to get the nose position as a function of time:

\[x_N(t) = \left[\frac{2}{\beta} \left( \frac{5k}{2 \beta} \right)^4 5V t^4 \right] ^\frac{1}{5} \propto t^\frac{4}{5}\]

and using this nose position we can establish the depth of the flow at the nose to be

\[h_N = \left( \frac{2 \beta}{5k} \right)^2 \left( \frac{x_N}{t} \right)^2 \propto t^{-\frac{2}{5}}\]

which is, interestingly, insensitive to the total volume of water from the storm (\(\propto V^\frac{2}{5}\)).

Overtopping the bank

A river flowing through the landscape may overtop its embankment, as shown in Fig. 3.23. This means water flows out of the channel and inundates the surrounding flood plane, and eventually can reach towns and other urban areas.

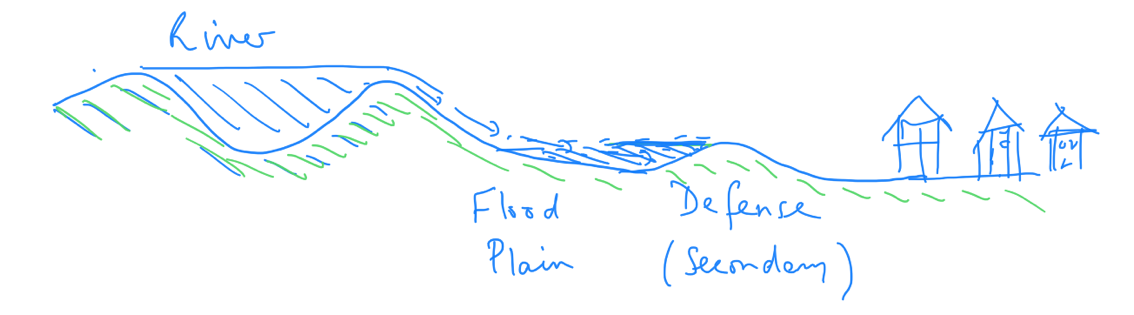
Fig. 3.23 A river overtopping its banks and flowing on to the flood plain.

We wish to determine the rate at which water is flowing out of the river. The situation is shown in more detail in Fig. 3.24.

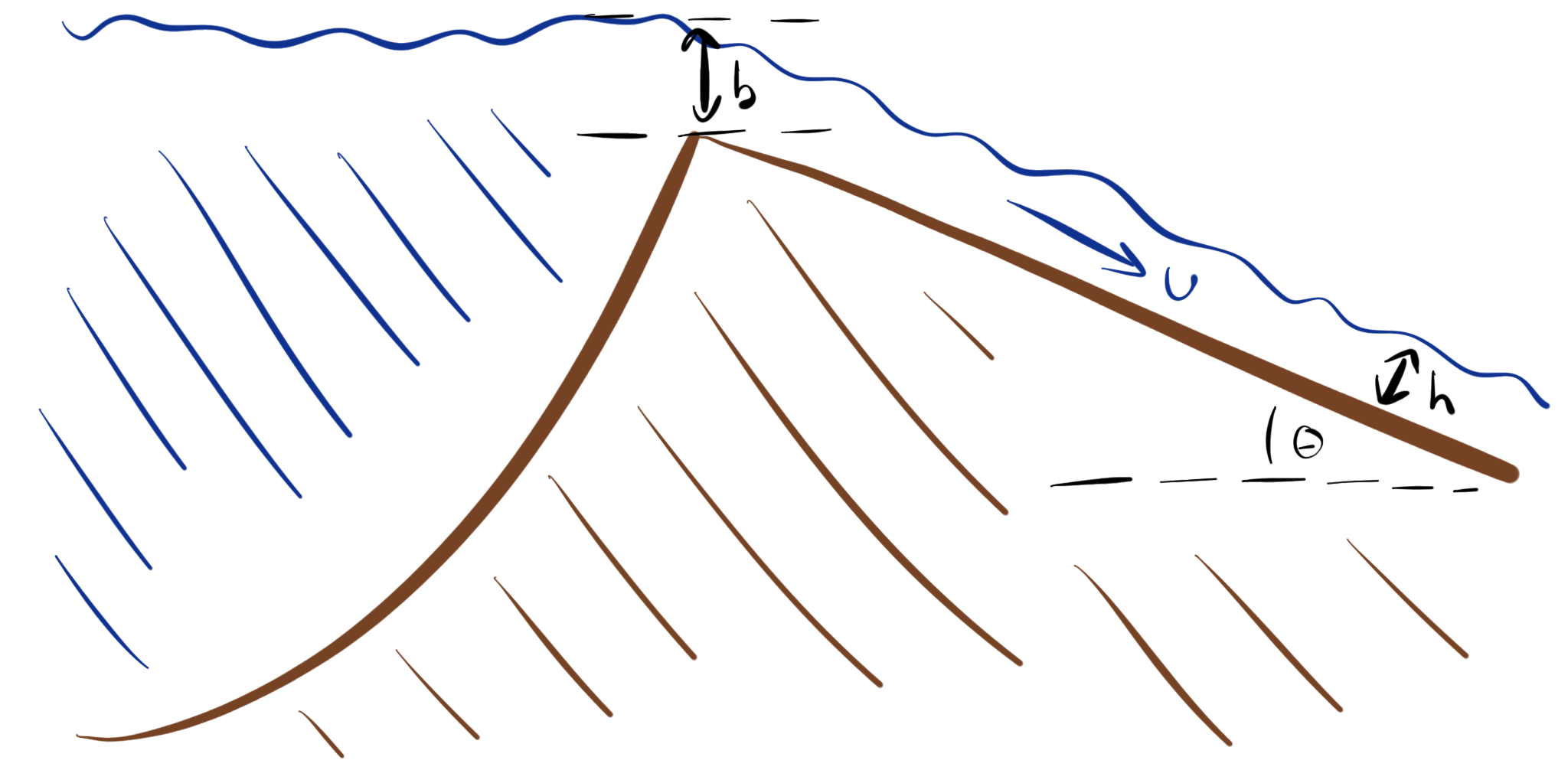
Fig. 3.24 A river overtopping its banks and flowing on to the flood plain.

The flow rate of the water moving over the embankment depends on the velocity of the water flow and the height over the top of the bank, \(b\). If the speed of the water is \(\sim \sqrt{gb}\) (as discussed in Section 3.3) then the flow rate per unit length along the embankment goes as

\[Q \sim \beta b \sqrt{g b}\]

where \(\beta\) is a geometric factor of \(\frac{2}{3\sqrt{3}}\) in the idealised case. With the flux over the bank established, we can turn our attention to the flow down the slope, further away from the levee.

Balancing the flows in and out of a control volume in the flow, as we have previously, we get a differential equation describing the rate of change of the thickness of the flow, \(h\):

(3.25)\[\pdv{h}{t} = -\pdv{Q}{x} + I\]

where \(I\) is an infiltration term. With rapid flow from the river, the flow is turbulent in the flooding zone, and the speed of the flooding water is given by

(3.26)\[u = \sqrt{\frac{gh \sin{\theta}}{C_D}}\]

and we can substitute into (3.25) using \(\pdv{Q}{x} = \pdv{(uh)}{x}\):

\[\pdv{h}{t} + \frac{3}{2} \sqrt{\frac{g \sin(\theta)}{C_D}} h^\frac{1}{2} \pdv{h}{x} - I = 0\]

So taking the steady state condition, \(\pdv{h}{t} = 0\) and integrating we get

\[h(x)^\frac{3}{2} - h(0)^\frac{3}{2} = - \sqrt{\frac{C_D}{g \sin(\theta)}} I x\]

and so we can see that \(h(x) \rightarrow 0\) when \(x \rightarrow \sqrt{\frac{C_D}{g \sin(\theta)}} \frac{h(0)^\frac{3}{2}}{I}\). \(I\) is small when the ground is waterlogged, and so \(x\) gets large, which holds with our general intuition about flooding.

With this model we can then assess how long the flood plain next to a river will take to fill up with water. If there is a secondary defence before the flood reaches the town along the river, as in the sketch, this flood plain provides a buffer to protect the town.

Non-examinable: derivation of \(\beta\)

If waters flood from a river, over the embankment, the flow rate of the water moving over the embankment depends on the height of the water in the centre of the river compared to the height at the embankment. If the water level decreases by an amount \(h\), the flow speed over the embankment is \(\sqrt{(gh)}\) and if the depth of the water is \(b\) at the embankment, the total flux is

\[Q = b(g h)^{1/2}\]

per unit length along the embankment. The height of the embankment below the height of the free surface of the river in the centre of the river above the river bed, \(H\), can be written as \(H-(b+h)\). At the crest of the embankment, the height above the base of the river is a maximum, and so if \(y\) is the coordinate normal to the river, then

(3.27)\[\dv{h}{y} + \dv{b}{y} = 0\]

If we differentiate the expression for the flux \(Q\) above with respect to \(y\), then the answer should be zero (as the flux is constant in space) and using Eq. (3.27) we then find that

\[2h = b\]

and so

\[3 h = (H_r - H_e)\]

Where \(H_r\) and \(H_e\) are the heights of the water surface in the centre of the river and the top of the embankment above the base of the river. This leads to the result that the flux is given by

\[Q = \frac{2}{3 \sqrt{3}} g^{1/2} (H_r - H_e) ^{3/2}\]

Where we can see we have approximated \((H_r - H_e) \sim b\) in the formula we used in the lectures.

Flood defense barriers

A flood defence barrier needs to withstand the pressure from the flood water. This leads to a horizontal force on the barrier which can be calculated from the integral of the hydrostatic pressure on the wall of the barrier.

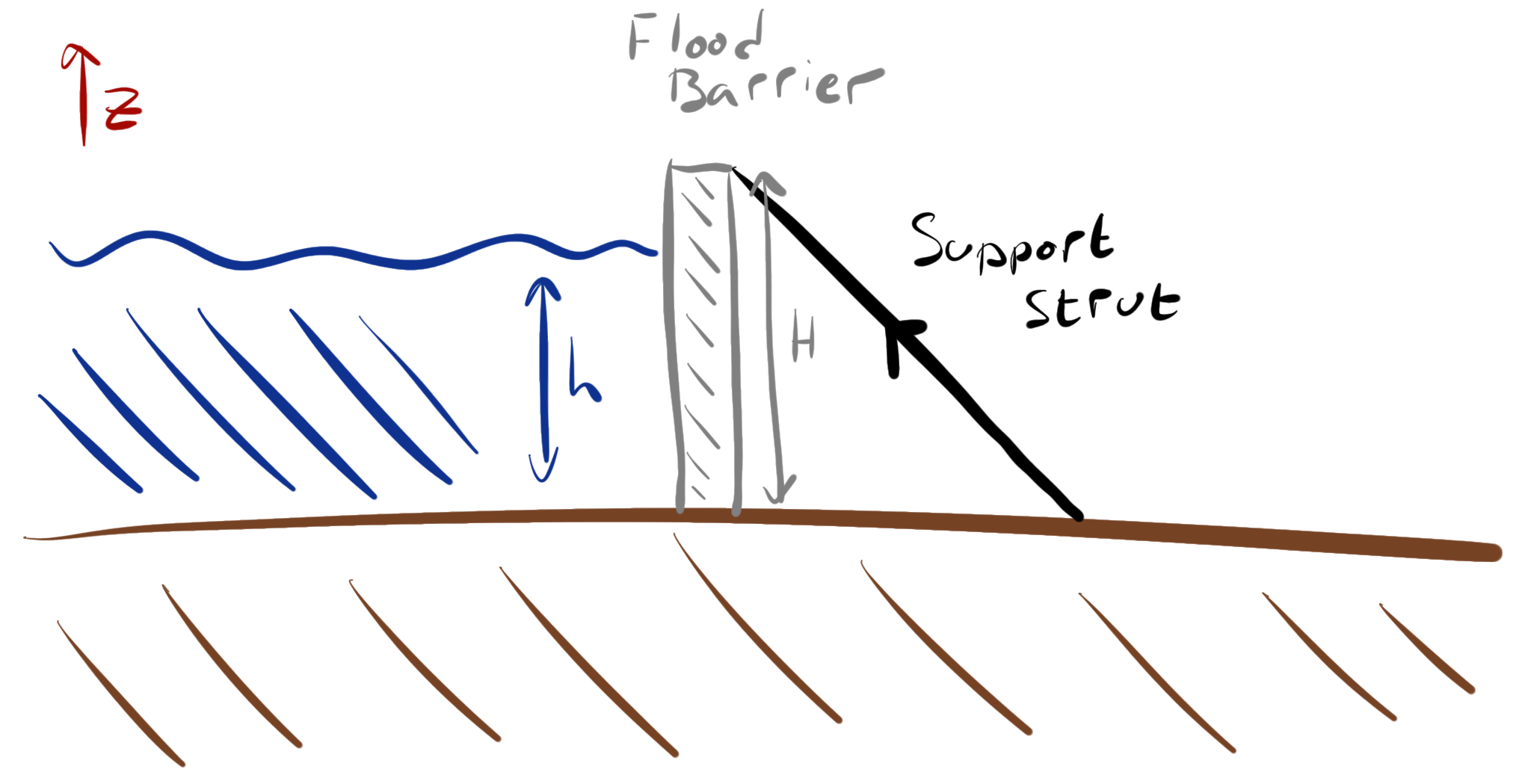
Fig. 3.25 A flood defence barrier, height \(H\), holding back water at a height \(h\).

Since the atmospheric pressure acts on both sides of the barrier, we can ignore it. Therefore, the net pressure acting at a point on the barrier as a function of \(z\) is

\[P(z) = \rho g (h-z)\]

and the total force acting will be

\[F = \int_0^h P(z) dz = \frac{\rho g h}{2}\]

A torque will also act on the barrier, which will be of the form

\[F = \int_0^h z P(z) dz\]

To prevent the barrier rolling over there needs to be a system to withstand this torque, which may include a series of inclined support rods pressing on the top of the barrier from the ground on the non—wet side of the barrier.

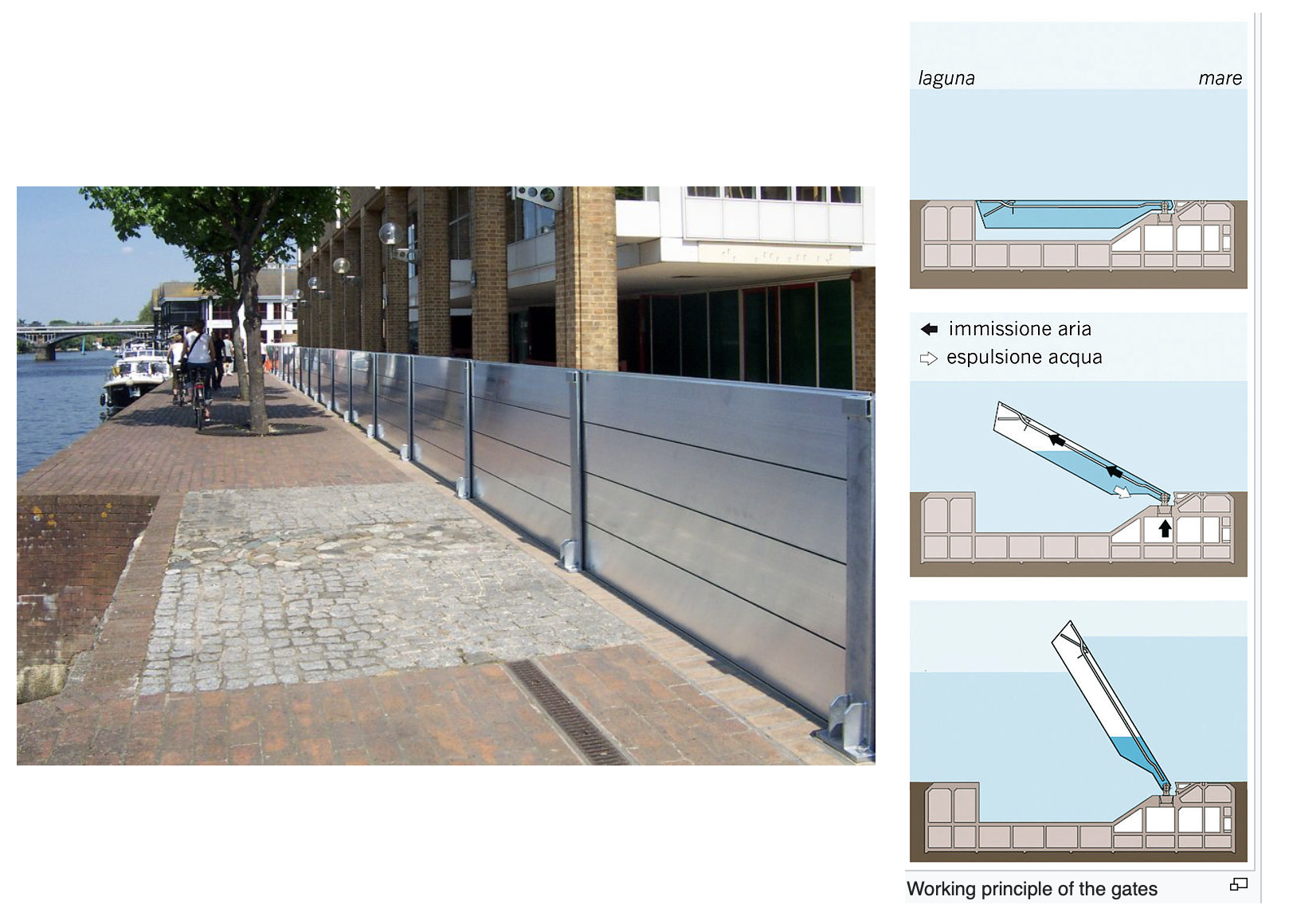
Fig. 3.26 In the Venice lagoon there are some interesting flood barriers which float up to the surface to stop incoming flow as in the figure above from the MODA website.