3.6. Flooding in urban environments

Objects carried by a flood

A particular challenge in a city environment for a flood relates to the transport of debris by a flood. Cars, logs and other large objects can be swept downstream and lead to blockages and the build up of very large forces by continuing floodwaters and damage.

There are several key elements to assessing the transport of an object by the flood which makes for an interesting calculation. For example, a static car without any flood water has a weight \(Mg\) balanced by an upward normal force \(N = Mg\). The sliding friction is typically given by a fraction \(\mu\) of this normal force, and so the critical force needed to move a dry car would be \(\mu Mg\).

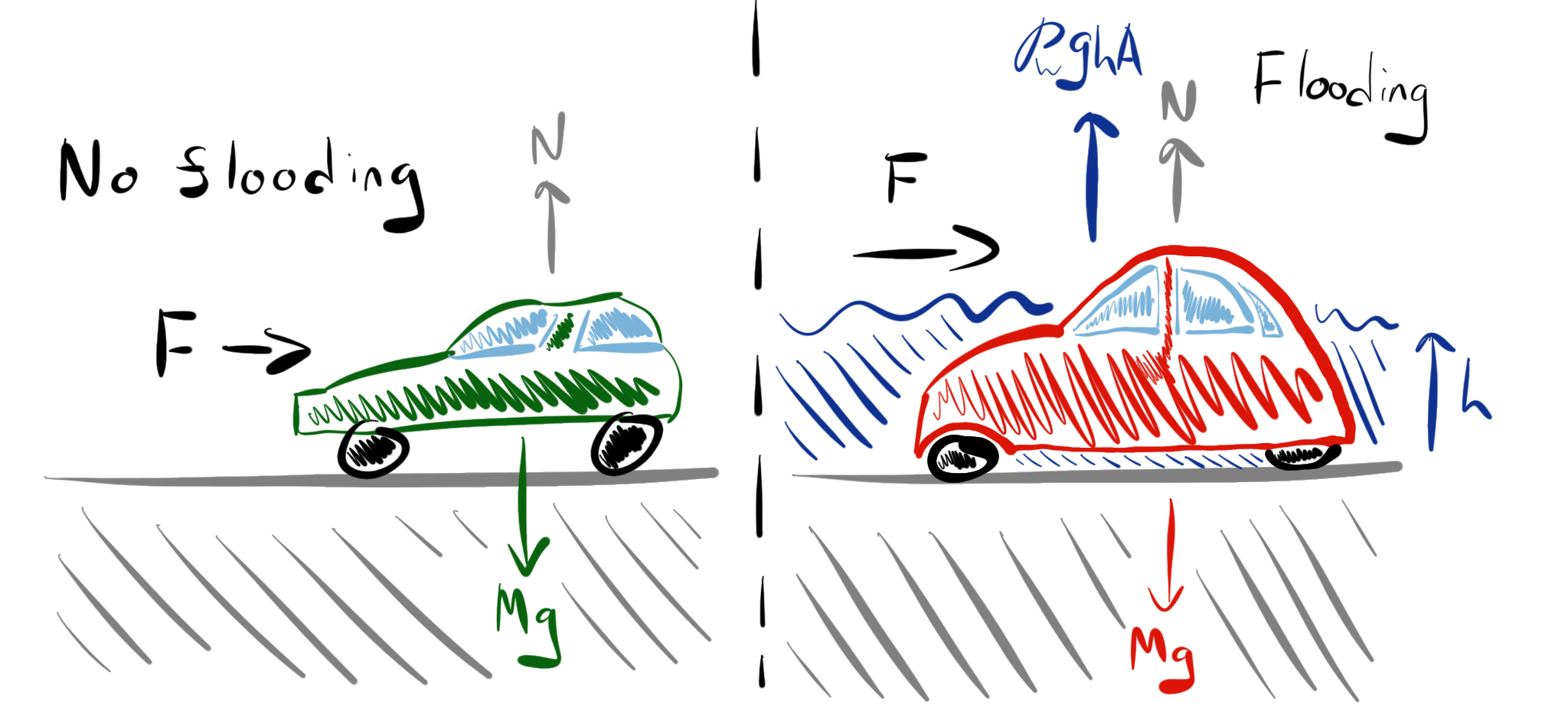
Fig. 3.27 The ability of a car to resist movement.

In a flood, if the car is submerged to a depth \(h\), and the car is waterproof then, modelling the car as a cuboid with a basal area \(A\), we find there is an upward buoyancy force, \(F_B\), from the water pressure acting on the base of the car given by

\[F_B = \rho g h A\]

Hence, the upward normal force from the ground is reduced and is now given by

\[N = M g - F_B\]

The horizontal force needed to move the car is now \(\mu (Mg – F_B)\) assuming that the coefficient of static friction is the same irrespective of the presence of the water. So, it is easier to move the car owing to the buoyancy from the presence of the water.

If the water flowing around the car has speed \(u\), then the force on the car will be

\[F = C_D \rho u^2 W h\]

where the width of the car is \(W\) and the water depth is \(h\) and \(C_D\) is the drag coefficient for the water flow round the car.

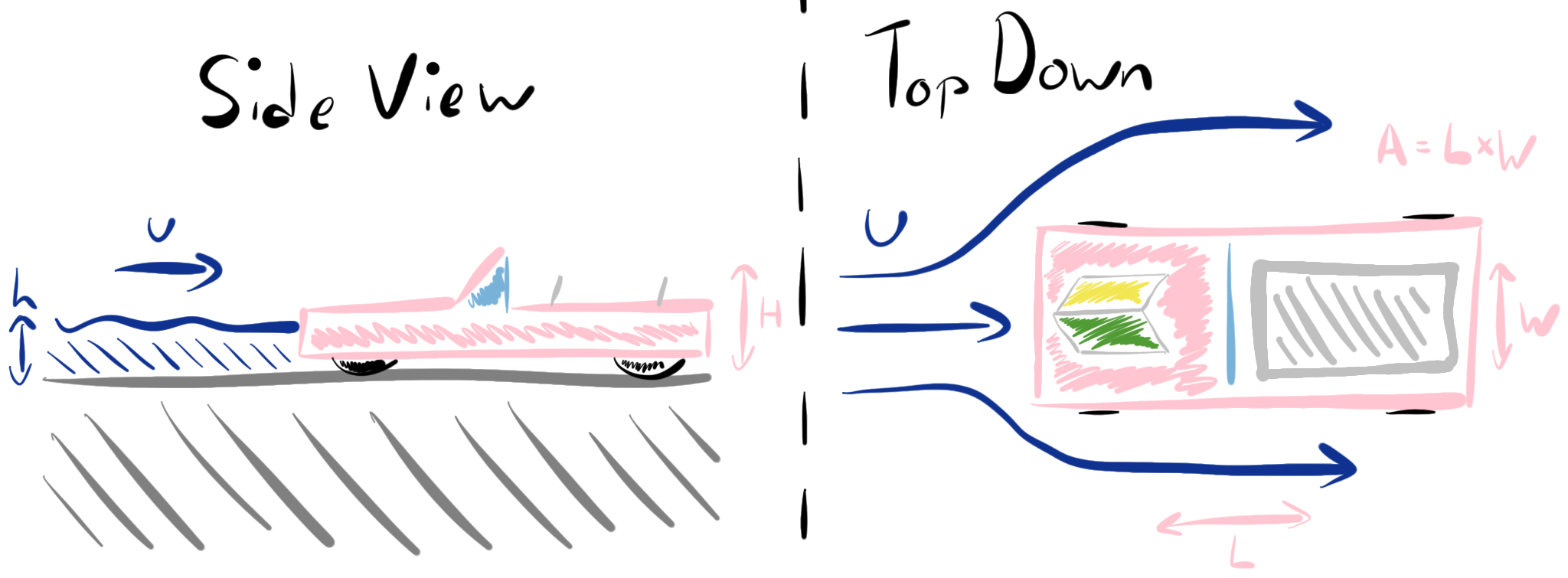
Fig. 3.28 Forces exerted on a car in a flood.

This leads to the result that the water speed required to move the car depends on the depth of the water according to the relation

\[C_D \rho u^2 W H = \mu (M g - \rho g h A)\]

Since \(M = AH \rho_c\) where \(\rho_c\) is the density of the car and \(H\) and the height of the car (the bulk density, which is about \(0.4-0.5 \mathrm{kg~m^3}\)) then with \(\mu = 0.2\), \(h = 0.5 \mathrm{m}\), \(A=3 \ \mathrm{m^2}\) and \(H = 1 \ \mathrm{m}\), we find the critical \(u\) has value of about \(1-2 \ \mathrm{m~s^{-1}}\).

If \(h\) increases towards \(0.5 \mathrm{m}\), then the buoyancy force is much greater, and the car is on the edge of floating off, so the drag force and hence current speed required to move the car falls to much smaller values.

Flooding through a city

When a flood passes through a city, the advance of the flood may be strongly controlled by the road system, which presents a high throughput pathway for the floodwaters. The development of the flood in the city will often encounter debris which can be picked up and transported by the flood, as illustrated in the calculations above, leading to significant blockages in the roads and hence time dependent evolution of the flood pathway.

In addition, the floodwaters can drain into the underground drains and sewer system from the road, and may then resurface downhill, depending on the flow capacity of the sewers/drains compared to the flux supplied by the flood. If the sewers spill out into the road this can lead to contaminants in the floodwaters; floodwaters can lead to significant health hazards in this context. The time of day that a flood enters a city is key for modelling the flood and the debris transported by the flood.

Groundwater floods

A somewhat similar flood process also occurs with groundwater flows in the event that there is an open permeable flow path, perhaps bounded below by a clay layer, as in the figure below. However, similar effects occur in limestone formations, but with much of the flow passing through the fracture-related permeability rather than the pore spaces.

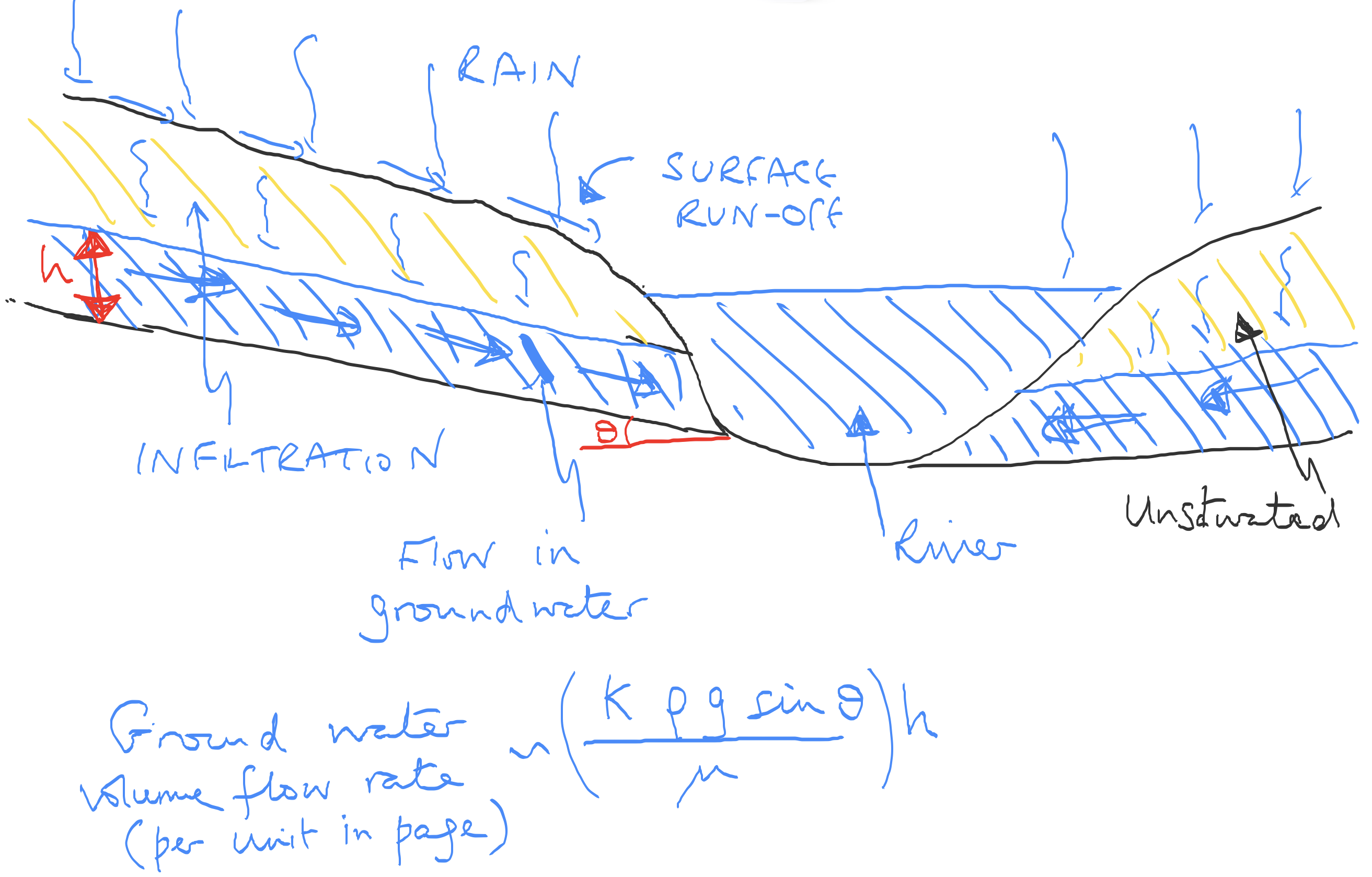
Fig. 3.29 The processes of a groundwater flood.

The flow running below ground typically has a velocity which depends on the permeability of the formation (e.g. soil) and the slope of the catchment. The flow may then drain into the base of a river. Analogous models for the groundwater flow can be developed to predict the flow into the river (see Example Sheet 2).

In some cases with limestone formations, the water table may rise very quickly leading to outflow from the side of hills, and this can lead to rapid flooding downstream.