6.9. Thermohaline Circulation

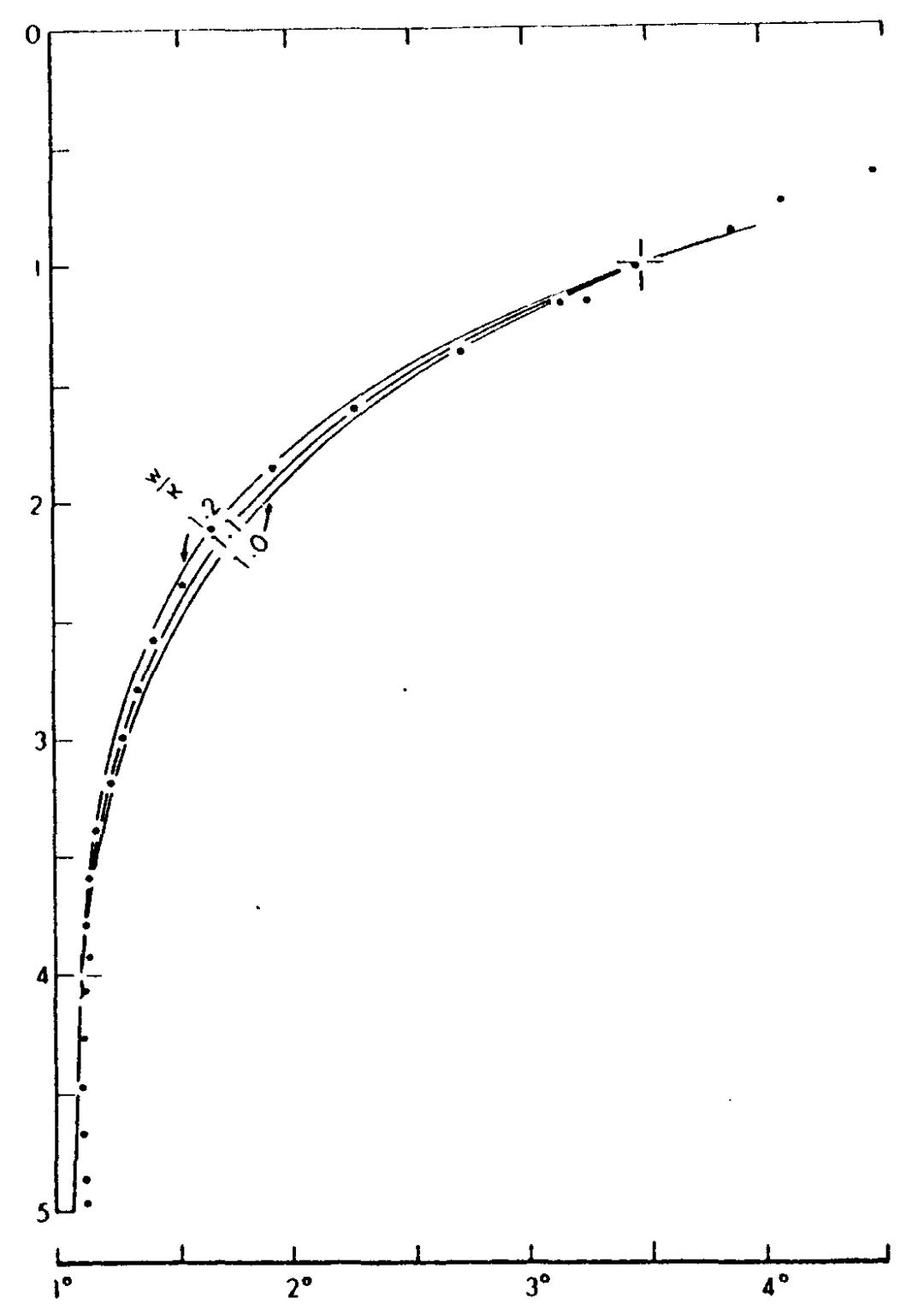
Fig. 6.33 Temperature measurements from the eastern Pacific ocean. The vertical axis indicates depth in km. From Munk, 1966.

Based on high latitude deep water formation, we might expect the deep ocean to fill up with the very cold water that sinks at high latitudes. To some extent this is true, but the as shown in Fig. 6.33, the temperature in the ocean interior is non-uniform and decreases gradually with depth. A remaining question is: if the cold water at the bottom of the ocean is gradually moving up, what is the source of heat that prevents the deep ocean from filling with the coldest water. Sunlight only penetrates the upper 10’s of meters, so solar heating cannot explain the observed temperature profile.

A solution to this problem was proposed by Munk, 1966. Munk proposed that downward mixing of heat by small-scale turbulence balances the upward advection of cold water. To model this, he used an advection/diffusion equation for a vertical profile of temperature, \(T(z,t)\) of the form

\[\frac{\partial T}{\partial t} + w\frac{\partial T}{\partial z} = \kappa \frac{\partial^2 T}{\partial z^2}.\]

At steady state, \(\partial T/\partial t=0\) and advection should balnce diffusion:

\[w\frac{\partial T}{\partial z} = \kappa \frac{\partial^2 T}{\partial z^2}.\]

If \(\kappa\) and \(w\) are constant, then this leads to solutions where the density is an exponential function of depth. Fig. 6.33 shows several exponential curves with different values of \(w/\kappa\) (labelled in units of km\(^{-1}\)).

Using radiocarbon data and estimates of sinking rates at high latitudes, Munk estimated that about \(Q\simeq 25 \times 10^{6} \mbox{m}^3/\mbox{s}\) upwell through a fixed depth globally. If we assume that this water upwells uniformly across the ocean area which is about \(A\simeq 4 \times 10^{14} \mbox{m}^2\), we get \(w=Q/A \simeq 6 \times 10^{-8} \mbox{m}/\mbox{s}\). Note that this is velocity is far too slow to measure directly.

Based on these estimates for the upwelling velocity and emprical fits to the temperature profiles in Fig. 6.33, Munk estimated that \(\kappa\simeq 10^{-4}\mbox{m}^2/\mbox{s}\). This is about 1000 times larger than the molecular diffusivity of heat in water, so eddying fluid motion is needed to accomplish this heat flux. In recent years, oceanographers have attempted to measure \(\kappa\) using tracers or by directly measuring turbulent motion. This work has converged on estimates near \(\kappa \simeq 10^{-5} \mbox{m}^2/\mbox{s}\), which is an order of magnitude smaller than Munk’s estimates. The reasons for this discrepancy still remain uncertain. One possbility which has recieved a lot of attention is that the upwelling does not occur uniformly throughout the ocean. Reserach into this question is still ongoing.

In the next section we will describe a box model that more explicitly represents the Thermohaline Circulation by adding a deep box to the Stommel model. This will also be the focus of the computing practical work. We will then use this model to study the ocean’s carbon system.